VALVE

Darlington and Sziklai pair 

Cascading of two bipolar transistors is commonly used to create a virtual transistor with high current gain. The transistors can be of the same polarity (Darlington, Fig. 1) or of the opposite polarities. The later configuration is called "Composite Darlington" or Sziklai pair (Fig. 2), as depicted below in a common emitter configuration.

                                                    Fig. 1

 

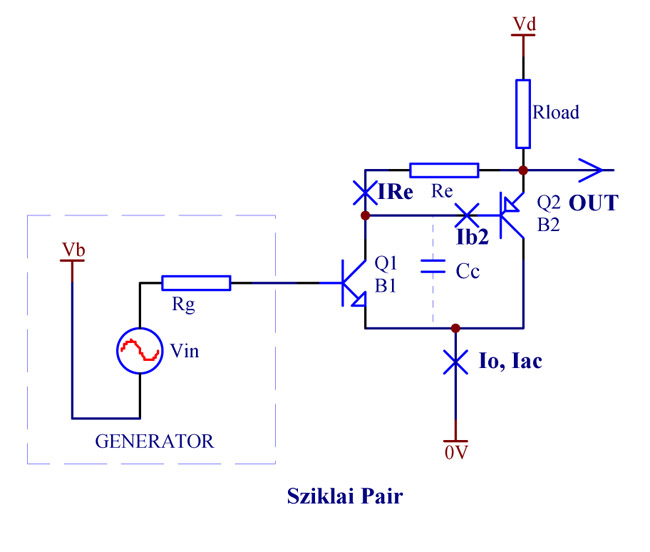
                                                             Fig. 2

 

Darlington and a Sziklai pair have much in common, but there are certain differences, especially if a resistor R_e is used for shunting the emitter junction of the second transistor Q2. The following discussion helps understand how R_e affects the performance of the two circuits. The following legend is used:

I_o -- quiescent (DC) current;

I_ac -- amplitude of the AC current component;

B₁, B₂ -- current gains of Q1 and Q2 respectively;

R_e -- resistor, shunting the emitter junction of Q2;

R_g -- output signal source impedance;

I_Re -- DC currents through R_e;

I_b2 -- Q2 base DC current;

C_c -- Q2 collector junction barrier capacitance.

 

1.  Reasonable range of R_e

Reduction of R_e causes the DC component through Q1 to rise, which in turn results in:

- transconductance (voltage gain) increase;

- input resistance reduction;

- slew rate and bandwidth increase;

- distortion reduction.

The smaller the R_e, the greater are the above listed effects, but only to a certain point. Once R_e becomes low enough and equal to the input resistance of Q2, further reduction of R_e results in the total current gain loss and defeats the purpose of the Darlington. Thus, minimum reasonable R_e is: 

R_emin = B₂ * 0.025V  / I_o                             (1)

Before analyzing the effect of R_e on the Darlington / Sziklai pair performance, it is convenient to introduce a "shunting factor" K_s,  which is a ratio of the current through R_e  to the Q2 base current I_b2 . 

K_s = I_Re / I_b2                                                 (2)

or

K_s = ( V_b * B₂ ) / (R_e * I_o )                           (3)

Here V_b is a typical voltage drop of a p-n junction. For silicon V_b = 0.6V. 

The lower the R_e, obviously the larger is the respective shunting factor K_s. The minimum reasonable R_e (from (1)) corresponds to the maximum reasonable shunting factor

 K_smax = V_b / 0.025V = 0.6V / 0.025V = 24.

Making I_Re more than 24 times greater than I_b2 serves no purpose.

For the same reasons, K_s shall be significantly smaller than B₂. Further reduction of R_e steers too much current away from Q2 base and is gradually turning a Darlington / Sziklai pair more and more into a single transistor Q1. With insufficient current through Q2, the later might enter AB class operation, which is not desirable. Eventually when R_e = 0, transistor Q2 gets completely disabled. 

Thus:

K_s < 24                                                 (4)

In practice K_s < 10...15.                     (4a)

and/or

K_s << B₂                                                (5),

whichever (4) or (5) dominates.

For high beta Q2, equation (4) prevails, for low beta Q2 -- (5) will have precedence. For practical purposes, "much less" sign in (5) means something about "less than 30...50% of". So:

K_s < (0.3...0.5) * B₂                              (5a)

 

2.  Current gain

Current gain of a Darlington is B₁*(B₂+1) + B₂. Current gain of a Sziklai pair is B₁*(B₂+1). This difference is immaterial, and it is common to assume that the compound beta B = B₁ * B₂. The compound beta is almost independent of the shunting resistor R_e, if the shunting resistor is above its reasonable minimum, in other words, if K_s << 24.

 

3.  Transconductance and input resistance

Without R_e, a Darlington has only 50% of the transconductance of a virtual super-beta single equivalent transistor. Here and below we will be often comparing a Darlington / Sziklai pair to this reference transistor with virtual B = B₁ * B₂. Consequently, input resistance is twice that of the equivalent transistor. This is because voltage gain of Q1 is about 0.5: 

S_D = 0.5 * I_o / 0.025V                          Z_Din = 2*  B₁ * B₂ * 0.025V / I_o           (6)

Transconductance and input resistance of a Sziklai pair exactly correspond to these of an equivalent reference transistor:

S_Z =  I_o / 0.025V ;                                  Z_Zin =  B₁ * B₂ * 0.025V / I_o                (7)

Adding the shunting resistor R_e or in other words, increasing shunting factor K_s leads to the transconductance rising and input resistance falling. For a classic Darlington (Fig. 1) these changes are insignificant, even for quite small R_e -- about 1.5...1.9 times, making the Darlington look almost exactly like a reference transistor (5), while for a Sziklai pair the change can be large:

S_Z =  ( I_o / 0.025V ) * (K_s + 1) ;              Z_Zin =  ( 0.025V / I_o ) * (B₁ * B₂) / (K_s + 1)        (8)

For that reason a Sziklai pair is preferred for amplification of small signals from a relatively low impedance source. Higher achievable transconductance of a Sziklai pair makes it useful as a low output impedance composite emitter follower. Apart from a popular application in the output stages of audio amplifiers, it is also useful in a simple voltage regulator with the following structure: Zener diode - RC noise filter - Sziklai pair.

Note that the equations are rather crude and assume K_s < 24, as was mentioned earlier.

 

4.  Slew rate and output capacitance

To allow for fast transitions of the output signal, enough current shall be available to charge and discharge the collector capacitance C_c of Q2. For the negative output transitions, the discharging current available through Q1 is virtually unlimited, but for the positive transitions supply of the charging current is limited. Without R_e, only I_b2 is available.

Slew rate = I_o / (B₂ * C_c).                       (9)

For example, with I_o = 1mA, B₂ = 200, C_c = 10pF, slew rate is 0.5V/µs, which is not great even for audio applications. Note that the slew rate limitation applies not only in a common emitter usage of the Darlington / Sziklai, but also to a common collector and common base. This should be kept in mind if a Darlington / Sziklai is to be used as booster follower in a "bootstrapped" gain stage (µ-follower) or as constant current source.

Reduction of R_e increases supply of the charging current and proportionally facilitates the slew rate:

Slew rate = (K_s + 1) * I_o / (B₂ * C_c).                       (10) 

Equations (9) and (10) apply to both Darlington and Sziklai pair, but for a Sziklai pair collector capacitances of Q1 and Q2 must be added together. Thus dynamic performance of a Sziklai pair is inferior compared to a classic Darlington.

In a Sziklai pair, junction capacitance C_c (C_c = C_c1 + C_c2) multiplied by B₂ results in a hefty equivalent output capacitance present across "emitter" and "collector" of a Sziklai pair. For example, if C_c = 15pF and B₂ = 100, output capacitance will equal to C_out = 1500pF. If such a Sziklai pair is used as an emitter follower, it is usually not a problem because of the low output impedance of such composite emitter follower. If the Sziklai pair is used in a common "base" configuration, for example, in a constant current source, then it is no problem either since the capacitive current is almost completely "recycled" from the collector back into the emitter.

However, if the Sziklai pair is used as a common emitter gain stage, this output capacitance might become a bandwidth limiting factor, depending on R_load.

Unfortunately for a Sziklai pair C_out is not affected by reduction of R_e.

But things are much better for a Darlindton -- reduction of R_e reduces the output capacitance. Besides, C_out is two times smaller for a start and does not include Q1:

C_out = C_c * B₂ / (K_s + 2)                        (11)

Note that in any case, if a wider bandwidth and/or higher slew rate is required, it is reasonable to choose Q2 with a lower beta.

 

5.  Distortion

Without R_e, a Darlington (Fig. 1) or a Sziklai pair (Fig. 2) is as dreadful in terms of distortion as a single transistor. Perhaps even worse, as beta dependence on current of the two transistors is compounded. However, for simplicity we will assume constant betas for both transistors Q1 and Q2.

Without R_e, for both both Darlington and Sziklai pair, in a common emitter configuration, distortion D equals:

D = ½ * (I_ac / I_o)                                                    (12)

This crude equation (12) takes only the second harmonic into account. Due to the exponential transfer function of a transistor the distortion depends only on the relative amount of AC component of the collector current. For example, if someone decides to make a single-ended class A power stage with say I_o = 50mA quiescent current, swinging from 25mA to 75mA with signal applied, the distortion will be 25%, though only 60mV of drive will be needed on the input (30mV for Sziklai pair).

An attempt to drive fully from 0mA to 100mA will result in 50% of distortion or so. Needless to say, transistors without feedback are not suitable for linear amplification.

When R_e is connected, the DC current through Q1 will increase, and the relative magnitude of AC component in the Q1 total current will reduce. Thus, voltage distortion in Q1 will drop. However, since in a Darlington (Fig. 1) both emitter junctions are connected in series, contribution of Q2 distortion will not change. So the gain will increase about 1.5...1.9 times, as has been mentioned earlier, the drive voltage will have to decrease in the same proportion and the distortion voltage referred to input will decrease in the same proportion, rendering the distortion unchanged.

Therefore in a Darlington (Fig. 1), distortion is not affected by R_e.

In contrast to a Darlington, Sziklai pair (Fig. 2) responds to R_e reduction quite well. For the analysis, the distortion of the Sziklai pair can be split into three components:

a) D₁ -- voltage distortion in Q1, which reduces with the reduction of R_e and consequent increase of DC current through Q1:

D₁ = ½ * (I_ac / I_o) * (1 / (K_s + 1))                                        (13) 

b) D₂ -- voltage distortion in Q2, referred to input, which increases with the reduction of R_e, because transconductance is rising while the distortion voltage reflected to input remains constant::

D₂ = ½ * (I_ac / I_o) * (0.025V * K_s / V_b)                                (14)

or with V_b = 0.6V :

D₂ = ½ * (I_ac / I_o) * (K_s / 24)                                                (14a) 

(Note again the same constant "24", related to the properties of silicon, as in (4)).

c) D₃ -- distortion in Q2, reflected to input as current and producing distortion in the signal source ("GENERATOR") output impedance R_g. Obviously, it is proportional to R_g and rises quadratically with R_e reduction:

D₃ = ½ * (I_ac / I_o) * (K_s² * R_g * I_o ) / (B₁ * B₂ * V_b)                            (15)

In the equation (15), "I_o" is not cancelled out deliberately, so that the first multiplicand " ½ * (I_ac / I_o) ", representing distortion of a single transistor, remains the same.

Very roughly:

D₃ / D₂ = R_g / Z_Zin ,                                                (16)

where Z_Zin -- input impedance of the Sziklai pair (8).

So the recipe for keeping input current distortion component D₃ at bay is simple and obvious: keep the source impedance R_g lower than input impedance of the Sziklai pair.

A plot in Fig. 3 illustrated how all the three components of distortion and the total distortion D_tot depend on the shunting factor, that is on R_e. The following conditions are used: I_o = 1mA, I_ac = 0.5mA, B₁ = 50, B₂ = 200, R_g = 15K.

 

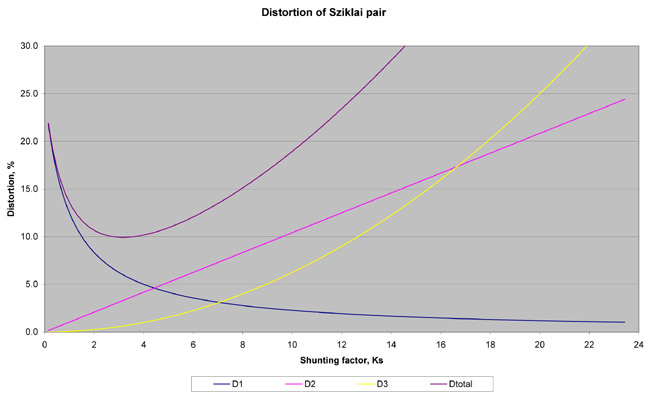
Fig. 3

in this case, a Sziklai pair can achieve about 2.2 times less distortion than a reference transistor or a classic Darlington (Fig. 1). The total distortion minimum is reached at about K_s = 3.5, in other words -- when the current through R_e is 3.5 times larger than the Q2 base current.

 

6.  Normalized distortion

Distortion figure in itself is not always the best characteristic of potential linearity of an amplifier. For instance, consider two amplifiers. One has gain of 10 and THD of 1%, while the other one -- gain of 100 and THD of 3%. Which one is more linear? The first one? Not necessarily. If we take the second amplifier and apply a negative feedback to reduce its excessive gain down to 10, its distortion will be reduced to 0.3%.

Thus, in order to compare potential linearity of some gain stages, one needs to fairly normalise the test results: normalise per unity gain, per unity transconductance, per unity output power (square root of), etc.

When dealing with a Darlington or a Sziklai pair, which is in effect a composite transistor-looking device, it is reasonable to normalise to the virtual reference super-beta equivalent single transistor with beta = B₁ * B₂ and the same quiescent current I_o.

Suppose we are reducing R_e (increasing K_s) in the Sziklai pair. Transconductance will increase beyond that of the reference transistor. Then we introduce a transconductance degenerating resistor (unbypassed "emitter" resistor) to bring the transconductance back to what the reference transistor would have had. This trick also brings the input resistance of the Sziklai pair back in line with the reference transistor. But now distortion of the Sziklai pair is reduced because of the negative feedback through the added emitter resistor. Thus we have exchanged the excessive transconductance for lower distortion. As a result, the Sziklai pair turned out a more linear device than a single super-beta reference transistor.

The plot below (Fig. 4) shows how R_e reduction (K_s increase) in a Sziklai pair brings down the normalised distortion.

Fig. 4

Ideally, with R_g = 0 the lower is the R_e -- the lower is the normalized distortion. It can be about 20 times less than of a reference transistor. In practice however, the rising current distortion component (D₃) associated with R_g, prevents the normalized distortion from decreasing monotonically. Beyond a certain point, which is K_s = 7.5 under the above conditions, the distortion begins to slowly rise. Yet the normalised distortion reduction is quite marked -- from 25% to about 2%.

 

7.  Conclusion

A Darlington (Fig. 1) and a composite Darlington (Sziklai pair) (Fig. 2) are the common techniques for creating a device similar to a super-beta transistor. Without a resistor R_e shunting the emitter junction of the second transistor of the pair, and at low frequencies, Sziklai pair is almost identical in performance to an equivalent super-beta transistor, while a Darlington has 50% of transconductance and double the input impedance.

Dynamic performance of the Darlington / Sziklai pair is inferior to that of a reference transistor -- slew rate is limited and hefty output capacitance appears across "emitter - collector" terminals of the composite devices.

Introduction of R_e modifies performance of the Darlington and Sziklai pair. When selecting R_e value, DC current through R_e shall not exceed 15...20 times the base current of the second transistor of the pair, even if beta of the second transistor is high.

Adding R_e greatly increases slew rate and reduces output capacitance of the classic Darlington (Fig. 1), while for a Sziklai pair (Fig. 2) affects only the slew rate.

As far as distortion is concerned, R_e has no effect on a Darlington, but can drastically reduce distortion and improve potential linearity of a Sziklai pair.

Transconductance can be exchanged for linearity. For example, a Darlington with a quiescent current of 50mA, driven from 5mA to 95mA would have 50% of THD, but it will have very high transconductance about 2000mA/V (quiescent). Connecting an unbypassed resistor in series with the "emitter" of the Darlington, one can lower its transconductance and increase linearity in the same proportion due to the negative feedback.

In this example, degenerating the transconductance from 2000mA/V to 5mA/V (by a 200 Ohm resistor) will result in THD of 0.13%. This THD is far lower than that of a vacuum tube, say 6V6GT, with the comparable transconductance.

This technique opens up an opportunity of creating Darlington vacuum tube replacements with lower distortion. Sziklai pair would give even better results with a lower R_e, but high-voltage high power PNP transistors are not readily available.